- Автор Abigail Brown [email protected].
- Public 2023-12-17 06:40.
- Последно модифициран 2025-01-24 12:03.
Регресията в Excel е начин за автоматизиране на статистическия процес на сравняване на няколко набора от информация, за да видите как промените в независими променливи влияят върху промените в зависимите променливи. Ако някога сте искали да намерите връзка между две неща, използването на регресионен анализ в Excel е един от най-добрите начини да направите това.
Инструкциите в тази статия се отнасят за Excel 2019, Excel 2016, Excel 2013, Excel 2010.
Какво е значението на регресията?
Регресията е подход за статистическо моделиране, който анализаторите използват за определяне на връзки между множество променливи.
Регресионният анализ започва с една променлива, която се опитвате да анализирате, и независими променливи, които тествате, за да видите дали засягат тази единична променлива. Анализът разглежда промените в независимите променливи и се опитва да съпостави тези промени с произтичащите промени в единичната (зависима) променлива.
Това може да звучи като разширена статистика, но Excel прави този сложен анализ достъпен за всеки.
Извършване на линейна регресия в Excel
Най-простата форма на регресионен анализ е линейната регресия. Простата линейна регресия разглежда връзката само между две променливи.
Например, следната електронна таблица показва данни, съдържащи броя на калориите, които човек е изял всеки ден, и теглото му през този ден.
Тъй като тази електронна таблица съдържа две колони с данни и едната променлива може потенциално да окаже влияние върху другата, можете да изпълните регресионен анализ на тези данни с помощта на Excel.
Активиране на добавката Analysis ToolPak
Преди да можете да използвате функцията за регресионен анализ на Excel, трябва да активирате добавката Analysis ToolPak в екрана с опции на Excel.
-
В Excel изберете менюто Файл и изберете Опции.

Image -
Изберете Добавки в лявото меню за навигация. След това се уверете, че Excel Add-ins е избрано в полето Manage.

Image -
Накрая изберете бутона Go.

Image -
В изскачащия прозорец на добавките. Активирайте Analysis ToolPack, като щракнете върху квадратчето пред него, за да добавите отметка и изберете OK.

Image
Сега, когато Analysis ToolPak е активиран, сте готови да започнете да правите регресионен анализ в Excel.
Как да извършите проста линейна регресия в Excel
Използвайки електронната таблица за тегло и калории като пример, можете да извършите линеен регресионен анализ в Excel, както следва.
-
Изберете менюто Данни. След това в групата Анализ изберете Анализ на данни.

Image -
В прозореца Анализ на данни изберете Regression от списъка и щракнете върху OK.

Image -
Входният диапазон Y е диапазонът от клетки, който съдържа зависимата променлива. В този пример това е теглото. Input X Range е диапазонът от клетки, който съдържа независимата променлива. В този пример това е колоната за калории.

Image -
Изберете Етикети за заглавните клетки и след това изберете Нов работен лист, за да изпратите резултатите в нов работен лист. Изберете OK, за да накарате Excel да изпълни анализа и да изпрати резултатите в нов лист.

Image -
Разгледайте новия работен лист. Резултатът от анализа има редица стойности, които трябва да разберете, за да интерпретирате резултатите.

Image Всяко от тези числа има следните значения:
- Множество R: Коефициентът на корелация. 1 показва силна корелация между двете променливи, докато -1 означава, че има силна отрицателна връзка. 0 означава, че няма корелация.
- R Square: Коефициентът на детерминация, който показва колко точки между двете променливи попадат на линията на регресия. Статистически това е сумата от квадратните отклонения от средната стойност.
- Коригиран R квадрат: Статистическа стойност, наречена R квадрат, която е коригирана за броя независими променливи, които сте избрали.
- Стандартна грешка: Колко точни са резултатите от регресионния анализ. Ако тази грешка е малка, тогава вашите регресионни резултати са по-точни.
- Наблюдения: Броят на наблюденията във вашия регресионен модел.
Останалите стойности в регресионния изход ви дават подробности за по-малките компоненти в регресионния анализ.
- df: Статистическа стойност, известна като степени на свобода, свързани с източниците на дисперсия.
- SS: Сума от квадрати. Съотношението на остатъчната сума на квадратите спрямо общия SS трябва да бъде по-малко, ако повечето от вашите данни отговарят на регресионната линия.
- MS: Среден квадрат на регресионните данни.
- F: F-статистиката (F-тест) за нулева хипотеза. Това осигурява значението на регресионния модел.
- Значение F: Статистическа стойност, известна като P-стойност на F.
Освен ако не разбирате статистика и изчисляване на регресионни модели, стойностите в долната част на резюмето няма да имат голямо значение. Въпреки това множеството R и R квадрат са двата най-важни.
Както можете да видите, в този пример калориите имат силна връзка с общото тегло.
Множествен линеен регресионен анализ в Excel
За да извършите същата линейна регресия, но с множество независими променливи, изберете целия диапазон (множество колони и редове) за Вход X диапазон.
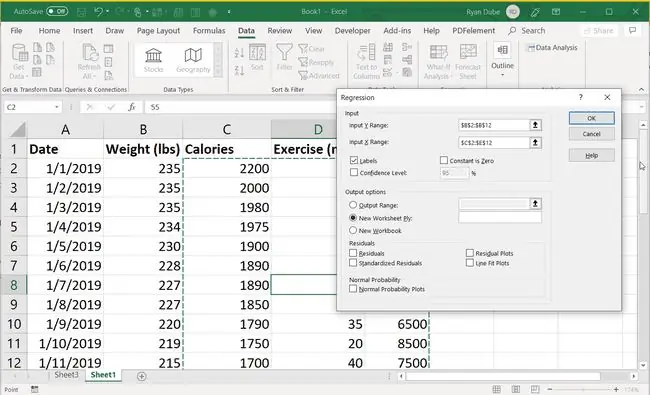
Когато избирате множество независими променливи, е по-малко вероятно да откриете толкова силна корелация, защото има толкова много променливи.
Въпреки това, регресионният анализ в Excel може да ви помогне да намерите корелации с една или повече от онези променливи, за които може да не осъзнавате, че съществуват, само като прегледате данните ръчно.






